Here’s a seemingly simple puzzle.

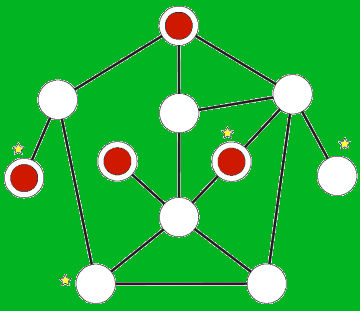
Place four coins on the bottom row of circles (G, D, E, and R), leaving the letters MARTIN exposed. Your challenge is to slide the coins along the paths joining the circles so that the four coins cover the top row of circles (M, T, I, and blank), exposing the letters GARDNER.
Sounds simple? The catch is that at no time are two coins allowed to be next to each other when a path joins the two circles. For example, you can’t move the G coin initially because the only allowed move would put it next to the D coin. The D coin can move to the T circle but not to the A circle or the I circle. You also have to slide the coins one at a time, all the way from one circle to another. And, where paths cross, you can’t switch from one path to another en route.
Robert A Hearn, a graduate student at the MIT Artificial Intelligence Laboratory, invented this puzzle in honor of Martin Gardner, mathemagician extraordinaire.
In traditional sliding-coin puzzles, a set of coins laid out in a certain arrangement must be slid into a new configuration in the fewest possible moves (see “Sliding-Coin Puzzles” at Sliding-Coin Puzzles). It’s been proved for these types of puzzles that it’s always computationally “easy” to determine whether a given puzzle is solvable.
Hearn’s Martin Gardner coin-sliding puzzle, however, is a different sort of beast. It’s more akin to sliding-block puzzles, such as the infamous 14-15 puzzle (see “Logic in the Blocks” at Logic in the Blocks), than to traditional sliding-coin puzzles.
It happens to take 25 moves to solve the Martin Gardner puzzle. In exploring how hard it might be solve such puzzles in general, Hearn discovered that there’s a relatively simple way to generate arbitrarily difficult instances. Indeed, it’s easy to make puzzles for which it’s computationally very difficult to determine whether there’s a solution at all.
More formally, it turns out the Hearn’s new type of puzzle belongs to a category of computational problems described as PSPACE-complete. This means that you should expect that, as the number of circles and paths gets larger, the amount of computer time required to solve the puzzle increases exponentially, even though the amount of memory required increases merely algebraically with size.
Here’s another puzzle for you to try.
Place four coins on the red circles. Slide the coins along the paths so that there is a coin on every starred circle. At no time may any two coins be adjacent—occupying two circles joined by a path. You should be able to solve this puzzle in 28 moves.
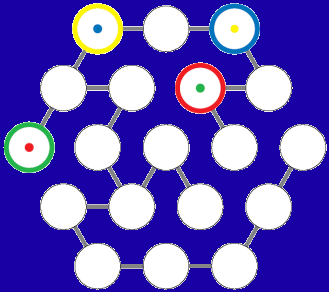
Hearn has tried a number of variations, such as using tokens or coins of different colors. “Then the start and end configurations have specific places for each color of token,” Hearn says. “This makes more complex puzzles possible on smaller graphs.” Mathematically, a graph is an array of vertices or nodes (circles in this case) connected by edges (paths).
In this puzzle, each of four tokens has a different color, as shown by the colored circles. Your goal is to move each token to the circle containing a dot of the same color. Solving this particular puzzle requires 116 moves.
Hearn’s Martin Gardner coin-sliding puzzle also inspired puzzle designer James Stephens, who runs the PuzzleBeast Web site (http://www.puzzlebeast.com/), to create a computer-generated set of puzzles called the “Meandering Monk Maze.” You can try them online at http://www.puzzlebeast.com/monkmaze/index.html.