Pouring M&Ms into a bowl leads to a marvel of packing efficiency, a team of sweet-toothed scientists reports.
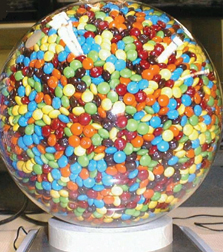

Using bench experiments and computer simulations, the team has found that squashed or stretched versions of spheres snuggle together more tightly than randomly packed spheres do.
This surprising result could help scientists better understand the behavior of disordered materials ranging from powders to glassy solids, says Princeton University chemist Salvatore Torquato. The finding could also lead to denser ceramic materials that might make for improved heat shields for furnaces and reduced-porosity glass with exceptional transparency.
He and his colleagues at Princeton, Cornell University, and North Carolina Central University in Durham detail their results in the Feb. 13 Science.
“This work is really beautiful,” comments Sidney R. Nagel of the University of Chicago. “It enhances our understanding of one of the outstanding questions in science”—namely, how densely various types of objects can pack together.
Investigations into arrangements of spheres date back centuries, but research into how efficiently aspherical objects aggregate has received scant attention.
In 1611, Johannes Kepler proposed that identical spheres can crowd together no more tightly than oranges do in a grocer’s stack, a formation called face-centered cubic packing. In the 19th century, Carl Friedrich Gauss weighed in with a partial proof of Kepler’s conjecture. Finally, in 1998, a mathematician offered a full proof, now widely accepted, that relies heavily on computer calculations (SN: 8/15/98, p. 103: http://www.sciencenews.org/sn_arc98/8_15_98/fob7.htm). The grocery store arrangement fills 74 percent of available volume.
“Since [an] ellipsoid is nothing more than a simple deformation of a sphere, we wanted to see what effect that simple change of shape would have on the packing efficiency,” Torquato explains. “The effect was dramatic and very unexpected.”
Using either plain, regular-size M&Ms or smaller versions known as minis, the scientists tested how efficiently the candies pack when poured into a square box roughly the size of a coffee mug or into a spherical flask up to 5 liters in volume. To confirm the randomness of the internal packing, the team took magnetic resonance imaging scans of a 5-liter flask filled with about 7,500 regular-size M&Ms.
Torquato and other colleagues had shown previously that random stacking of spheres fills markedly less space—about 64 percent—than does the grocery arrangement (SN: 4/1/00, p. 219: Available to subscribers at Random packing of spheres). For both actual and simulated ellipsoids, Torquato and his colleagues now find that random packings fill as much as 73.5 percent of the space, just a smidgeon less than hand-stacked spheres do.
Why is random packing denser for ellipsoids than for spheres? The team proposes that the asymmetric ellipsoids can tip and rotate in ways that spheres can’t, so an ellipsoid nestles close to more neighbors than a sphere does. Indeed, the team finds that as many as 11 neighbors touch an ellipsoid, whereas each tight-packed sphere typically has only 6 adjacent neighbors.
Theoretical physicist Samuel F. Edwards of Cambridge University in England says, “It’s a real advance to do [packing experiments and simulations] on ellipsoids.”
For such experiments, Torquato says, M&Ms make “great” test objects because they’re inexpensive and uniform in size and shape. What’s more, he adds, “you can eat the experiment afterwards.”






